Queuing theory scrutinizes the entire system of waiting in line, including elements like the customer arrival rate, number of servers, number of customers, capacity of the waiting area, average service completion time, and queuing discipline. Queuing discipline refers to the rules of the queue, for example whether it behaves based on a principle of first-in-first-out, last-in-first-out, prioritized, or serve-in-random-order.
PROBABILITY THEORY AND RANDOM PROCESSES UNIT I: PROBABILITY AND RANDOM VARIABLES PART- A 1. MATHEMATICAL OR APRIORI definition of probability. Let S be the sample space and A be an event associated with a random experiment. Let n(s) and n(A) be the number of elements of ‘S’ and ‘A’. Then the probability of an. Explore queuing theory for scheduling, resource allocation, and traffic flow applications Queuing theory is the mathematical study of waiting lines or queues. This approach is applied to different types of problems, such as scheduling, resource allocation, and traffic flow.
2. How did queuing theory start?
Queuing theory was first introduced in the early 20th century by Danish mathematician and engineer Agner Krarup Erlang.

Erlang worked for the Copenhagen Telephone Exchange and wanted to analyze and optimize its operations. He sought to determine how many circuits were needed to provide an acceptable level of telephone service, for people not to be “on hold” (or in a telephone queue) for too long. He was also curious to find out how many telephone operators were needed to process a given volume of calls.
His mathematical analysis culminated in his 1920 paper “Telephone Waiting Times”, which served as the foundation of applied queuing theory. The international unit of telephone traffic is called the Erlang in his honor.
Queuing Theory Examples Problems
MA8402 Notes Probability And Queuing Theory Regulation 2017 Anna University free download. Probability And Queuing Theory Notes MA8402 pdf free download.

OBJECTIVES: MA8402 Notes Probability And Queuing Theory
To provide necessary basic concepts in probability and random processes for applications such as random signals, linear systems in communication engineering.
To understand the basic concepts of probability, one and two dimensional random variables and to introduce some standard distributions applicable to engineering which can describe real life phenomenon.
To understand the basic concepts of random processes which are widely used in IT fields.
To understand the concept of queueing models and apply in engineering.
To understand the significance of advanced queueing models.
To provide the required mathematical support in real life problems and develop probabilistic models which can be used in several areas of science and engineering.
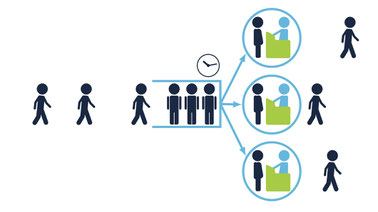
OUTCOMES: MA8402 Notes Probability And Queuing Theory
Upon successful completion of the course, students should be able to: Understand the fundamental knowledge of the concepts of probability and have knowledge of standard distributions which can describe real life phenomenon. MA8402 Notes Probability And Queuing Theory
Understand the basic concepts of one and two dimensional random variables and apply in engineering applications. Apply the concept of random processes in engineering disciplines. Acquire skills in analyzing queueing models. Understand and characterize phenomenon which evolve with respect to time in a probabilistic manner
TEXTBOOKS: MA8402 Notes Probability And Queuing Theory
1. Gross, D., Shortle, J.F, Thompson, J.M and Harris. C.M., ―Fundamentals of Queueing Theory”, Wiley Student 4th Edition, 2014.
2. Ibe, O.C., ―Fundamentals of Applied Probability and Random Processes”, Elsevier, 1st Indian Reprint, 2007.
REFERENCES : MA8402 Notes Probability And Queuing Theory
Applications Of Queuing Theory
1. Hwei Hsu, “Schaum‘s Outline of Theory and Problems of Probability, Random Variables and Random Processes”, Tata McGraw Hill Edition, New Delhi, 2004.
2. Taha, H.A., “Operations Research”, 9th Edition, Pearson India Education Services, Delhi, 2016.
3. Trivedi, K.S., “Probability and Statistics with Reliability, Queueing and Computer Science Applications”, 2nd Edition, John Wiley and Sons, 2002.
4. Yates, R.D. and Goodman. D. J., “Probability and Stochastic Processes”, 2nd Edition, Wiley India Pvt. Ltd., Bangalore, 2012. MA8402 Notes Probability And Queuing Theory
| Subject name | Probability And Queuing Theory |
| Short Name | PQT |
| Semester | 4 |
| Subject Code | MA8402 |
| Regulation | 2017 regulation |
MA8402 Probability And Queuing Theory NotesClick Here To Download
